编译原理

第二章 文法和语言

• 程序设计语言

  • 语法：一种规则，用它可以形成和产生一个合适的程序。阐明语法的工具是文法。

  • 语义

    • 静态语义：一系列的限定规则，并确定哪些合乎语法的程序是合适的。
    • 动态语义：运行语义或执行语义，表明程序要做什么，要计算什么。

文法的直观概念

• 当我们表述一种语言时，就是要说明这种语言的句子。

  • 如果语言只含有有穷多个句子，则只需穷举列出句子的有穷集。
  • 如果语言含有无穷多个句子，存在着如何给出它的有穷表示的问题。这需要一种规则，用这些规则来描述语言的结构，可以把这些规则看成一种元语言，这些规则(或语言)就称为文法。

符号和符号串

• 字母表：元素的非空集合，也称为符号集
• 符号：字母表中的元素

• 符号串：由字母表中的符号组成的任何有穷序列

  • 长度：如果某符号串x有m个符号，称其长度为m，表示为|x|=m
  • 空符号串：不包含任何符号的符号串，用|ε|=0表示

• 符号串的头尾，固有头和固有尾：如果z=xy是一符号串，那么x是z的头，y是z的尾。如果x是非空的，那么y是固有尾；若y非空，x是固有头。

  • 头尾都有空串

  • 如：符号串abc

    • 头： ε, a, ab, abc
    • 尾：abc，bc, c, ε
    • 固有头： ε, a, ab
    • 固有尾： bc, c, ε
• 符号串的连接：设x和y是符号串，它们的连接xy是把y的符号写在x的符号之后得到的符号串
• 符号串的方幂：设x是符号串，把x自身连接n次得到符号串z，即z=xx…xx，成为符号串x的方幂，写作$z=x^n$
• 符号串集合：若符号串集合A中的一切元素都是某字母表上的符号串，则称A为该字母表上的符号串集合。

• 符号串集合的乘积：AB={xy|x∈A且y∈B}。即AB是满足x∈A，y∈B的所有符号串xy所组成的集合

  • 对于任意符号串，有εx=xε=x
• •集合的闭包：指定字母表Σ之后，用Σ表示Σ上的所有有穷长的串的集合。Σ称为集合Σ的闭包。$Σ*=Σ^0 \cup Σ^1 \cup Σ^2 \cup … \cup Σ^n…$
• 集合的正闭包：$Σ^+=Σ^1 \cupΣ^2 \cup… \cupΣ^n…$称为Σ的正闭包。
• Σ具有无穷数量的元素，如果x是Σ中的元素，则表示为$x\in \Sigma^{*}$，否则$x \notin \Sigma^{*}$ 。对于所有的Σ，有ε∈Σ。

• 规则（重写规则，产生式或生成式）的定义：

  形如α→β或α∷=β的(α，β)有序对，α称为规则的左部，β称作规则的右部

文法

• 定义2.1：文法G定义为四元组$(V_N,V_T,P,S )$其中

  • N代表Nonterminal,T代表Terminal
  • $V_N$为非终结符号(或语法实体，或变量)集；
  • $V_T$为终结符号集；
  • P为规则(α→β)的集合，$α\in(V_N \cup V_T )^{*}$且至少包含一个非终结符，$β\in(V_N \cup V_T)^{*}$ ；
  • $V_N$，$V_T$和P是非空有穷集。
  • S称作识别符号或开始符号，它是一个非终结符，至少要在一条产生式中作为左部出现。
  • $V_N$和$V_T$不含公共的元素，即$V_N \cap V_T = Φ$
  • 用V表示$V_N V_T$ ，称为文法G的字母表或字汇表

• 一般约定的写法：

  • 第一条产生式的左部是识别符号
  • 用尖括号括起来的是非终结符，不用尖括号括起来的是终结符
  • 或者用大写字母表示非终结符，小写字母表示终结符。
  • 常用符号：→ ∷= | < >

  • 各种写法：

    • G：S→0S1 S→01
    • G[S]： S→0S1 S→01
    • G[S]: S→0S1 | 01

• 直接推导

  • 定义：设α→β是文法$G[V_N,V_T, P, S]$的产生式，γ和δ是V*中的任意符号，若有符号串v, w满足：v=γαδ,w=γβδ,则称v(应用规则α→β)直接产生w,或说，w是v的直接推导，或说，也称w直接归约到v，记作$v \Rightarrow w$

• 推导

  • 定义：若存在直接推导的序列：$v = w_0 \Rightarrow w_1 \Rightarrow ... \Rightarrow w_n=w,(n>0)$,则记为$v \overset{+}{\Rightarrow} w$，v推导出w，或w归约到v，推导长度为n

  • 定义：若有$v \overset{+}{\Rightarrow} w$，或v=w，则记为$v \overset{*}{\Rightarrow} w$

    句型和句子

• 定义：设G[S]是一文法，如果符号串x是从识别符号推导出来的，即有$S\overset{*}{\Rightarrow}x$，则称x是文法G的句型。若x仅由终结符号组成，即$S\overset{*}{\Rightarrow}x,x\in{V_T}^{*}$，则称x是文法G的句子。
• 定义：文法G所产生的语言定义为集合$\{x|S \overset{*}{\Rightarrow} x, x \in {V_T}^{*}\}$。用L(G)表示。
• • X是句型
  • X仅由终结符号组成
• 若L（G1）=L（G2），则称文法G1和G2是等价的。

文法的类型

• 0型文法

  • •设文法$G=(V_N,V_T,P,S)$，若P中任一产生式α→β，都有$α\in(V_N \cup V_T)^{*}$且至少含有一个非终结符，而$β \in (V_N \cup V_T)^{*}$，则G是一个0型文法。
  • 0型文法也称短语文法。0型文法的能力相当于图灵机。或者说，任何0型语言都是递归可枚举的；反之，递归可枚举集必定是一个0型语言。
  • 没有限制的产生式规则

• 1型文法

  • 设文法$G=(V_N,V_T,P,S)$，若P中任一产生式α→β，都有|β|≥|α|，仅仅S → ε除外，则G是一个1型文法或上下文有关文法。
  • •其他定义方法：设文法G[S]，若P中任一产生式α→β的形式为α1A α2 → α1 β α2，其中α1 ，β，$ α_2 \in (V_N \cup V_T)^*$， β≠ε，$A \in V_N$
  • 产生式的左侧至少有一个非终结符， 且左侧不得比右侧长

• 2型文法

  • 设文法$G=(V_N,V_T,P,S)$，若P中任一产生式α→β，满足：α是一个非终结符， $β \in (V_N \cup V_T)^*$ ，则G是一个2型文法或上下文无关文法。
  • 有时将2型文法的产生式表示为A→β的形式，其中$A \in V_N$，也就是说用β代替非终结符A时，与A所在的上下文无关，因此取名为上下文无关
  • 每个产生式的左侧至少有一个非终结符

• 3型文法

  • 设文法$G=(V_N,V_T,P,S)$，若P中每一个产生式都是A→aB或A→a，其中A和B都是非终结符，$a \in {V_T} \cup \{ε\}$ ，则G是一个3型文法或正规文法。
  • 产生式的右侧只能是一个终结符， 或者一个终结符跟一个非终结符

• 四种文法之间的关系

  

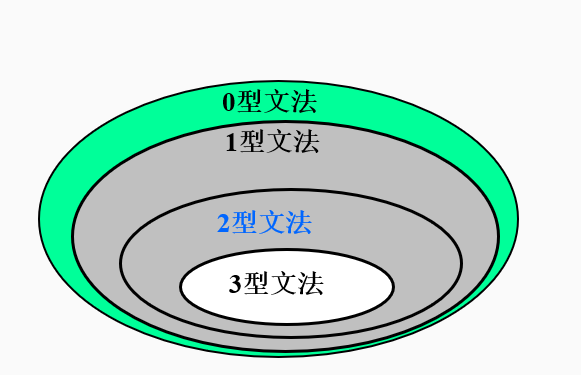
文法和语言

• 0型文法产生的语言称为0型语言
• 1型文法或上下文有关文法产生的语言称为1型语言或上下文有关语言
• 2型文法或上下文无关文法产生的语言称为2型语言或上下文无关语言

• 3型文法或正则（正规）文法产生的语言称为3型语言或正则（正规）语言

  上下文无关文法及其语法树

• 上下文无关文法有足够的能力描述程序设计语言的语法结构

语法树

• 设$G=( V_N,V_T,P,S)$为一上下文无关文法，若对于G的任何句型都能构造与之关联的语法树(推导树)。这棵树满足下面四个条件：

  • 每个结点都有一个标记，此标记是V的一个符号
  • 根的标记是S
  • 若一结点n至少有一个它自己除外的子孙，并且有标记A，则肯定$A \in V_N$
  • 如果结点n有标记A,其直接子孙结点从左到右的次序是n1，n2，…，nk，其标记分别为A1，A2，…，Ak，那么A→A1A2，…，Ak一定是P中的一个产生式
• 语法树的结果：从左至右读出推导树的叶子标记
• 语法树表示了在推导过程中施用了哪个产生式和在哪个非终结符上，它并没有标明使用产生式的顺序。

最左推导和最右推导

• 最左（最右）推导：在推导的任何一步$α \Rightarrow β$，其中α、β是句型，都是对α中的最左（右）非终结符进行替换
• 最右推导被称为规范推导
• 由规范推导所得的句型称为规范句型

文法的二义性

• 若一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的
  或者，若一个文法存在某个句子有两个不同的最左（右）推导，则称这个文法是二义的
• 自然语言是二义性语言。
• 判定任给的一个上下文无关文法是否二义，或它是否产生一个先天二义的上下文无关语言，这两个问题是递归不可解的，但可以为无二义性寻找一组充分条件
• 文法可以经过改写，从而构造出一个等价的无二义文法

句型的分析

• 句型的分析是识别一个符号串是否为某文法的句型，是某个推导的构造过程。进一步说，当给定一个符号串时，试图按照某文法的规则为该符号串构造推导或语法树，依此识别出它是该文法的一个句型，当符号串全部由终结符号组成时，就是识别它是不是某文法的句子。
• 对于程序设计语言来说，我们要识别程序设计语言的程序，程序是定义程序设计语言的句子。在语言的编译实现中，把完成句型分析的程序称为分析程序或识别程序，分析算法又称识别算法。

• 从左到右的分析算法：总是从左到右地识别输入符号串，首先识别符号串中的最左符号，进而识别右边的一个符号。分为两大类：

  • 自上向下：从文法的开始符号出发，反复使用各种产生式，寻找“匹配”于输入符号串的推导。

    • 自上而下方法是从文法符号开始，将它做为语法树的根，向下逐步建立语法树，使语法树的结果正好是输入符号串
    • 在自上而下的分析方法中如何选择使用哪个产生式进行推导？

  • 自下而上：从输入符号串开始，逐步进行“归约”，直至归约到文法的开始符号

    • 自下而上方法则是从输入符号串开始，以它做为语法树的结果，自底向上地构造语法树
    • 在自下而上的分析方法中如何识别可归约串？

短语和句柄

• 短语：每个非终结符最后推导出终结符符号串是相对于这个非终结符的短语

  • 找到某语法树的所有非叶结点为根的子树，该子树的叶结点从左向右组成的符号串是对应于该子树的根结点的短语

• 一个非终结符直接一步推导出来的终结符是相对于这个非终结符的句柄

  • 在查找短语过程中，如果该子树为两层，则该短语为对应于该子树的根结点的直接短语。

文法实用中的一些说明

• 文法中不含有有害规则和多余规则

  • 有害规则：形如U→U的产生式。会引起文法的二义性
  • 多余规则：指文法中任何句子的推导都不会用到的规则

• 文法中不含有不可到达和不可终止的非终结符

  • 文法中某些非终结符不在任何规则的右部出现，该非终结符称为不可到达。
  • 文法中某些非终结符，由它不能推出终结符号串，该非终结符称为不可终止。

• 对于文法G[S]，为了保证任一非终结符A在句子推导中出现，必须满足如下两个条件：

  • A必须在某句型中出现
  • 必须能够从A推出终结符号串t来

• 上下文无关文法中某些规则可具有形式A→ε，称这种规则为ε规则

  因为ε规则会使得有关文法的一些讨论和证明变得复杂,有时会限制这种规则的出现

  两种定义的唯一差别是ε句子在不在语言中

  • 文法构思的启示是要找出语言的有穷描述，而如果语言L有一个有穷的描述，则L1=L∪｛ε｝也同样有一个有穷的描述，并且可以证明，若L是上下文有关语言、上下文无关语言或正规语言，则L∪｛ε｝和L-｛ε｝分别是上下文有关语言、上下文无关语言和正规语言。
• 若L是由文法G=(VN,VT,P,S)产生的语言，P中的每一个产生式的形式均为A→α，其中$A \in V_N$，$α \in (V_N \cup V_T)^*$ ，则L能由这样一种文法产生，即每一个产生式或者为A→Β形式，其中A为一非终结符，即$A \in V_N$，$β \in (V_N \cup V_T)^+$ ，或者为S→ε形式，且S不出现在任何产生式的右边。
• 如果$G=(V_N,V_T,P,S)$是一个上下文有关文法，则存在另外一个上下文有关文法G1，它所产生的语言与G产生的相同，其中G1的开始符号不出现在任何产生式的右边。又如果G是一个上下文无关文法，也能找到一个上下文无关文法G1，如果G是一个正规文法，则也能找到这样一个正规文法G1。